Cuando analizamos series temporales en finanzas o economía, como precios de acciones, inflación o demanda, la estacionariedad es un concepto clave. Una serie no estacionaria puede llevar a resultados engañosos o “regresiones espurias”, mientras que una serie estacionaria permite construir modelos más precisos y confiables.

En este artículo aprenderás, de forma clara y práctica, qué significa que una serie sea estacionaria, qué son las raíces unitarias y cómo verificarlas en R usando tests como Dickey-Fuller Aumentado (ADF) y Phillips-Perron (PP). Además, veremos cómo transformar una serie no estacionaria en estacionaria paso a paso.

¿Qué es la estacionariedad en una serie temporal?

Como mencionamos en el post anterior sobre series temporales, una serie temporal es estacionaria cuando la media y la variabilidad se mantienen constantes a lo largo del tiempo, es decir, no es en función del tiempo; y además, no presenta tendencia.

Por tanto, para dar respuesta a la pregunta ¿Qué es una serie temporal estacionaria? Se puede decir: una serie temporal estacionaria es aquella cuya media, varianza y autocorrelación permanecen constantes a lo largo del tiempo. En otras palabras, su comportamiento estadístico no cambia con el paso del tiempo.

En este sentido, aquí nos centramos en la media, varianza y autocorrelación.

Para entenderlo mejor, veamos los siguiente gráficos, los cuales me parecieron muy ilustrativos y son tomados de la web Analytics Vidhya:

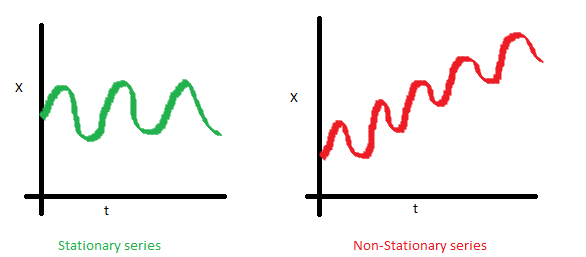
Como se puede apreciar, la serie temporal del lado izquierdo presenta una media constante, mientras que la de la derecha presenta tendencia, con una media que se incrementa con el paso del tiempo.

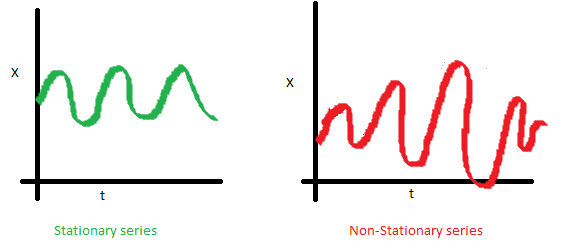
Como observamos, en la imagen anterior, la gráfica del lado izquierdo es estacionaria, mientras que la del lado derecho presenta una variabilidad que aumenta con el nivel de la serie, lo que se conoce como heterocedasticidad.

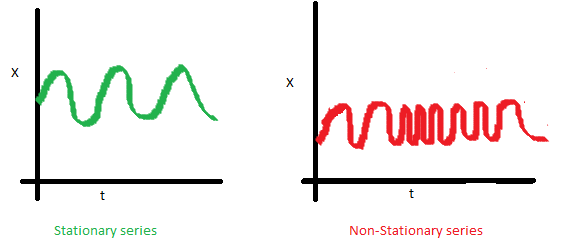
En la imagen anterior, se observa una serie estacionaria en el lado izquierdo, y en el derecho una serie con autocovarianza que está en función del tiempo.

¿Por qué es importante que las series temporales sean estacionarias?

Porque, en la mayoría de modelos y análisis de series temporales, es indispensable que éstas sean estacionarias, parten bajo éste supuesto. Cuando no es el caso, el primer requisito suele ser estacionariedad, lo cual se suele conseguir aplicando logaritmos (para corregir heterocedasticidad), diferencia regular (eliminar tendencia), diferencia estacional (eliminar componente estacional), etc. Entonces a partir de aquí, intentar construir modelos estocásticos para poder predecir la serie.

Hay que tener en cuenta que regresiones con MCO y variables no estacionarias pueden generar regresiones espurias, esto es, regresiones con estimadores sesgados y donde se obtiene un R² alto y altos t-estadísticos; pero en estos casos, el criterio convencional para juzgar si hay una relación causal entre las variables no es confiable y aunque dichos estadísticos y R² sean estadísticamente significativos realmente no existe una relación.

Para ejemplificar; modelos estacionarios, suelen referirse a los modelos de medias móviles y modelos ARMA; en cuanto a modelos no estacionarios, encontramos los modelos ARIMA, ARCH y GARCH.

Ahora, vamos a realizar algunos test estadísticos para comprobar si la serie es estacionaria o no, y para ello, vamos a seguir trabajando con la serie del post anterior, el dataset que trae por defecto R (R Project) sobre pasajeros mensuales de las aerolíneas internacionales en el período comprendido entre 1949 y 1960, el dataset se llama “AirPassengers”.

Al comprobar con “class”, observamos que nos arroja un objeto de la clase “ts”, equivalente a “time series”.

data(AirPassengers)

Pasajeros <- AirPassengers
class(Pasajeros)

## [1] "ts"

Si queremos saber los estadísticos principales:

summary(Pasajeros)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   104.0   180.0   265.5   280.3   360.5   622.0

Graficamos la serie:

plot(Pasajeros)

Tal como habíamos analizado en el post anterior, en el gráfico podemos observar que la serie tiene tendencia, heterocedasticidad y un componente estacional, los cuales tratamos aplicando logaritmos y diferenciando la serie.

Ahora, para entender mejor lo anterior, graficamos descomponiendo la serie:

plot(decompose(Pasajeros))

En el último gráfico, claramente se puede observar la tendencia y el componente estacional.

¿Raíz unitaria?

Así que ahora, vamos a realizar tests de raíces unitarias, para analizar las propiedades de la estacionariedad, teniendo presente que cuando una serie o proceso tiene raíz unitaria, la serie no es estacionaria y los estimadores MCO no tienen distribución normal.

Una raíz unitaria, es una tendencia estocástica en la serie temporal. Algunas veces se le llama “paseo aleatorio con deriva”. Por tanto, si la serie tiene una raíz unitaria, ésta presenta un patrón sistemático que es impredecible.

Entonces, una serie temporal es estacionaria si un cambio en el tiempo no cambia la forma de la distribución; y las raíces unitarias son una causa de no estacionariedad.

Existen dos procedimientos comunes para remover la tendencia de una serie temporal (1) primeras diferencias (2) regresión tendencial. Las primeras diferencias suelen ser apropiadas para series temporales integradas de orden uno -I(1)-; mientras que la regresión tendencial es apropiada para series con estacionariedad tendencial I(0). Los tests de raíces unitarias pueden ser usados para determinar si una serie con tendencia primero deber ser diferenciada o hacer una regresión tendencial, esto es, si hay estacionariedad tendencial o diferencial.

• El test de Dickey-Fuller Aumentado (Augmented Dickey-Fuller Test (ADF), en inglés), elimina la autocorrelación e indica si una serie es estacionaria o no.
• El test de Phillips–Perron (PP), es una modificación de test de Dickey-Fuller. Este test corrige la autocorrelación y heterocedasticidad en los errores.

Para aplicar los tests anteriores, vamos a usar el paquete “tseries”.

En estos tests, la hipótesis nula es que la serie tiene raíces unitarias, por tanto, no es estacionaria. Por ende, la hipótesis alternativa es que la serie es estacionaria (alternative=“stationary”) y k, corresponde al orden de lags o retrasos.

Con un p-valor inferior a 0.05, la hipótesis nula se suele rechazar.

Veamos el test de Dickey-Fuller Aumentado “adf.test”:

library(tseries)
adf.test(diff(log(Pasajeros)), alternative="stationary", k=0)

## 
##  Augmented Dickey-Fuller Test
## 
## data:  diff(log(Pasajeros))
## Dickey-Fuller = -9.6003, Lag order = 0, p-value = 0.01
## alternative hypothesis: stationary

Como se puede observar, después de aplicar logaritmos y diferenciar la serie, ahora sí es estacionaria; un p-valor de 0.01, indica que rechazamos la hipótesis nula de no estacionariedad.

Ahora, aplicamos el test de PP:

pp.test(diff(log(Pasajeros), alternative="stationary"))

## 
##  Phillips-Perron Unit Root Test
## 
## data:  diff(log(Pasajeros), alternative = "stationary")
## Dickey-Fuller Z(alpha) = -93.215, Truncation lag parameter = 4,
## p-value = 0.01
## alternative hypothesis: stationary

Con este test, también se obtuvo un p-valor de 0.01, por tanto, rechazamos la hipótesis nula y aceptamos la alternativa, y podemos decir que la serie es estacionaria.

Por último, vamos a realizar nuevamente el gráfico donde descomponemos la serie, pero esta vez la serie transformada:

plot(decompose(diff(log(Pasajeros))))

Después de analizar los anteriores tests y observar la última gráfica, se puede decir que no se observa tendencia en la serie transformada.

Por otro lado, para tratar la estacionalidad, se puede tomar una diferencia estacional, es decir, calcular la diferencia entre el valor de la serie en un mes con respecto al dato de ese mismo mes, pero del año anterior o aplicar un ajuste estacional, procedimiento que se se puede ver en mi entrada sobre desestacionalizar series temporales con R.

Conclusión: la importancia de comprobar la estacionariedad

Comprobar la estacionariedad y la presencia de raíces unitarias no es solo un paso técnico: es la base para realizar un análisis de series temporales sólido. Una serie no estacionaria puede distorsionar tus resultados, pero con herramientas como ADF, Phillips-Perron y las transformaciones adecuadas (logaritmos, diferencias, ajustes estacionales) puedes garantizar modelos predictivos más confiables.

💡 Tip: Antes de aplicar modelos ARIMA, ARCH o GARCH en R, asegúrate siempre de verificar la estacionariedad. Te ahorrará errores y mejorará la precisión de tus predicciones.